Mathematics and Art

I confess I surprised myself when I check out from our local library a video course on mathematics, but the title Joy of Thinking: The Beauty and Power of Classical Mathematical Ideas caught my attention.  And I was totally intrigued with every lesson.  To my delight, the course explores how math can be used as a tool to explore aesthetics and the mysteries of nature.

Some folks think it is not logical that artists could be fascinated by mathematics.  Somewhere in the mix of professional mandates, artists are told that logic and art don’t mix, to use logic is to stifle creativity.  Art is suppose to come altogether from the intuition, they say.  Leave logic to the mathematicians. As a result of this kind of thinking, art and math get pigeon-holed as poles apart when, in fact, there is a lot of intuition in mathematics, and artists and architects have been depending upon mathematical proportions for centuries.

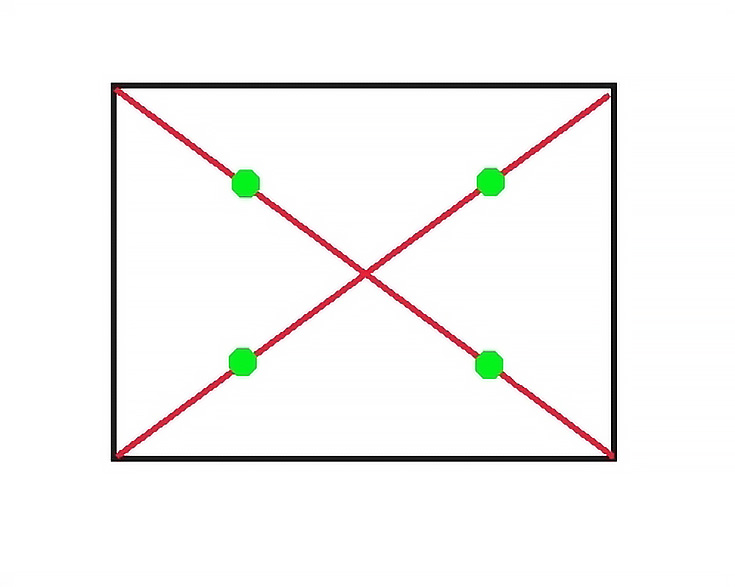
One obvious way artists use mathematical proportion is when we locate a rectangle’s "sweet spots" (eyes of the rectangle) for placing our centers of interest.  We have discovered that those four areas midway a canvas' center and each of its corners are ideal spots for placing points of emphasis.

I've shown these with the green dots in the diagram below.

Qiang Huang has used the lower right "sweet spot" for placing the orange in his painting, "Out of Shadow."

Carolyn Anderson uses the same location for placing the hands in her painting, "Boy Reading."

I admit that if we artists had to do the math to come up with these "sweet spots," we'd refuse to deal with it, but the beauty of it is that hundred of years ago mathematicians figured out where these are: they discovered the Golden Rectangle on which the "sweet spots" are based.  

Fibonacci who lived in the 1200's AD discovered a sequence of numbers that show the logic of the Golden Rectangle.  It begins with 0  followed by 1 and here is where the sequence begins. The next number in the sequence, 1,  is the results of the first two added together (0 + 1).  That 1 is added to the first 1 to get 2, then the 2 is added to this 1 to get the next number 3. Then 3 is added back to the previous number (2) to equal 5, then 5+3=8, then 8+3=11 and on and on so that the sequence looks like this:  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584 and on and on: there is no end to it.  This sequence is exciting because it represents a ratio pattern that is found throughout nature, whether spirals in seashells, leaf arrangement on plants, scales of a pineapple, or all living cells.  (For more on this, go HERE.)

Here's how it sets up the Golden Rectangle:

Slight disclaimer:  the squares here are not exact, but illustrate  the point.

The formation begins with 2 squares the same size (1 and 1 in the illustration above) .  Add another square (2) whose edges are the same length as the combination of the first two together. Add a third square whose edges are the length of 2 + 1, a fourth whose edges are the length of  3 + 2, another whose edges are the same as 3 + 5 and on and on.  This rectangle could continue until it circles the earth a zillion times.  When built on this sequence, it is an infinite rectangle, the Golden Rectangle. Perhaps its perfection is in its infinitude.

I often wonder whether there is a strong relationship between intuition and infinity.  Whether there is or not, it's all fun to think about.  Perhaps logic and intuition are two sides of the same coin. But that's a discussion for another day.  Meanwhile, I hope you enjoyed this little mental exercise.